Stochastic Processes: mudanças entre as edições

De Pontão Nós Digitais
Ir para navegaçãoIr para pesquisar
Sem resumo de edição
m (moved prev periods)
 
(24 revisões intermediárias pelo mesmo usuário não estão sendo mostradas)
Linha 1: Linha 1:
This is the main page of an undergraduate-level course in stochastic processes targeted at engineering students (mainly computer engineering and its interface with mechanical engineering), being taught in 2021 condensed PAE (emergential semester during the COVID-19 pandemic) at the Polytechnic Institute [http://pt.wikipedia.org/wiki/IPRJ IPRJ]/UERJ.
This is the main page of an undergraduate-level course in stochastic processes targeted at engineering students (mainly computer engineering and its interface with mechanical engineering), being taught in 2024 (2024.2 period) at the Polytechnic Institute [http://pt.wikipedia.org/wiki/IPRJ IPRJ]/UERJ.


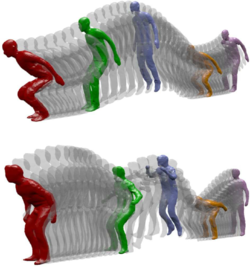
Previous periods: [[Stochastic_Processes_2021_condensed|2021 condensed]]


[[Image:Mocap_transfer.png|right|250px|thumb|Recent application of [https://en.wikipedia.org/wiki/Gaussian_process Gaussian stochastic processes] for 3D motion capture transfer [http://openaccess.thecvf.com/content_cvpr_2017/papers/Boukhayma_Surface_Motion_Capture_CVPR_2017_paper.pdf (CVPR 2017)] ]]
[[Image:Mocap_transfer.png|right|250px|thumb|Recent application of [https://en.wikipedia.org/wiki/Gaussian_process Gaussian stochastic processes] for 3D motion capture transfer [http://openaccess.thecvf.com/content_cvpr_2017/papers/Boukhayma_Surface_Motion_Capture_CVPR_2017_paper.pdf (CVPR 2017)] ]]
Linha 12: Linha 11:
== General Info ==
== General Info ==
* Instructor: prof. [http://rfabbri.github.io Ricardo Fabbri], Ph.D. Brown University
* Instructor: prof. [http://rfabbri.github.io Ricardo Fabbri], Ph.D. Brown University
* Meeting times (exercises): Tuesdays 1:20pm-3:10pm, room 206; Thursdays 1:20pm - 3:10pm, room 208.
* Chat: IRC #labmacambira for random chat
* Chat: IRC #labmacambira for random chat


Linha 40: Linha 38:
* ''An Introduction to Stochastic Modeling'', Taylor & Karlin
* ''An Introduction to Stochastic Modeling'', Taylor & Karlin
* ''Pattern Theory: The Stochastic Analysis of Real-World Signals'', David Mumford and Agnes Desolneux - the first chapters already cover many types of stochastic processes in text, signal and image AI [[Image:Mumford-book.jpg]]
* ''Pattern Theory: The Stochastic Analysis of Real-World Signals'', David Mumford and Agnes Desolneux - the first chapters already cover many types of stochastic processes in text, signal and image AI [[Image:Mumford-book.jpg]]
* My own machine learning and computational modeling book draft, co-written with prof. Francisco Duarte Moura Neto and focused on diffusion processes on graphs like PageRank. There is a probability chapter which is the basis for this course. We have many copies at [[IPRJ]]'s library.
* My own machine learning and computational modeling book draft, co-written with prof. Francisco Duarte Moura Neto and focused on diffusion processes on graphs like PageRank. There is a probability chapter which is the basis for this course.  


==== Other books to look at ====
==== Other books to look at ====
Linha 99: Linha 97:
=== Assignment 0 ===
=== Assignment 0 ===
* Exercise 1.1 of the main book
* Exercise 1.1 of the main book
* Suggested due date: Before thursday of the 1st week.
* Suggested due date: Before thursday of the 2nd week.


=== Assignment 1 ===
=== Assignment 1 ===
Linha 105: Linha 103:
''Simulating Discrete Random Variables'' (pp 51, 52, 53)
''Simulating Discrete Random Variables'' (pp 51, 52, 53)
* No need to read this book for this exercise. You will review discrete random variables in the context of Markov chains for natural language processing; this is basic for most AI bots nowadays. If you're curious about the applications, you can read the book chapter just for fun.
* No need to read this book for this exercise. You will review discrete random variables in the context of Markov chains for natural language processing; this is basic for most AI bots nowadays. If you're curious about the applications, you can read the book chapter just for fun.
* Suggested due date: Before 2nd meeting of the 2nd week.
* Suggested due date: Before Thursday of the 3rd week.


=== Assignment 2: Exercise list for chapter 1 ===
=== Assignment 2: Exercise list for chapter 1 ===
7 Exercises: 1.3, 1.5, 1.6, 1.7, 1.9, 1.10, 1.19
7 Exercises: 1.3, 1.5, 1.6, 1.7, 1.9, 1.10, 1.19
* Suggested due date: Before 2nd meeting of the 2nd week.
* Suggested due date: at least 1 week before P1 (suggested)


=== Assignment 3: Exercise list for chapter 2 ===
=== Assignment 3: Exercise list for chapter 2 ===
11 Exercises: 2.1, 2.4, 2.6, 2.8, 2.9, 2.10, 2.12, 2.14, 2.15, 2.18
11 Exercises: 2.1, 2.4, 2.6, 2.8, 2.9, 2.10, 2.12, 2.14, 2.15, 2.18
Computer: 2.26
Computer: 2.26
* Due date: Before 1st meeting of the 3rd week
* Due date: before P1 (suggested)


=== Assignment 4: Exercise list for chapter 3 ===
=== Assignment 4: Exercise list for chapter 3 ===
Linha 122: Linha 120:
=== Assignment 5: Exercise list for chapter 5 (MCMC) ===
=== Assignment 5: Exercise list for chapter 5 (MCMC) ===
4 Exercises: 5.1, 5.2, 5.5, 5.6
4 Exercises: 5.1, 5.2, 5.5, 5.6
* Due date: before 2nd meeting 1 week after P2.
* Due date: before P2 (suggested)


=== Assignment 6: Exercise list for chapter 6 ===
=== Assignment 6: Exercise list for chapter 6 ===
2 Exercises: 6.3, 6.4
4 Exercises: 6.3, 6.4, 6.7, 6.8
2 Bonus exercises (extra grading): 6.7, 6.8
* Due date: before P2 (suggested)
* Due date: before 2nd meeting 2 weeks after P2.


== Exams ==
== Exams ==
* '''P1:''' 17ago21
* '''P1:''' ter19set23
* '''P2:''' 31ago21
* '''P2:''' ter17out23
* '''Final-Sub:''' 2ago21
* '''Final-Sub:''' ter19dez2


== Evaluation criteria ==
== Evaluation criteria ==
See course plan on moodle, tab "Boas-vindas".
<pre>
P = (P1 + P2)/2
 
if P >= 5 --> passa direto
 
Trabalhos serão dados após a P1 de acordo com a demanda da turma, sendo a pontuação inclusa na P2.
 
Final F opcional
 
M = (F + P)/2 para os que fizerem final
 
if M >= 5 --> passa
else reprova
</pre>


== Awesome Links ==  
== Awesome Links ==  
Linha 155: Linha 165:
== Keywords ==
== Keywords ==
random fields, stochastic modeling, data science, queue theory, machine learning, poisson process, markov chains, Gaussian processes, Bernoulli processes, soft computing, random process, Brownian motion, robot path planning, artificial intelligence, simulation, sampling, pattern formation, signal processing, text processing, image processing, dimentionality reduction, diffusion, Markov Chain Monte Carlo MCMC, tracking, branching process, stochastic calculus, SDEs
random fields, stochastic modeling, data science, queue theory, machine learning, poisson process, markov chains, Gaussian processes, Bernoulli processes, soft computing, random process, Brownian motion, robot path planning, artificial intelligence, simulation, sampling, pattern formation, signal processing, text processing, image processing, dimentionality reduction, diffusion, Markov Chain Monte Carlo MCMC, tracking, branching process, stochastic calculus, SDEs
== See Also ==
Previous periods: 2023 (see wiki history) [[Stochastic_Processes_2022.2|2022.2]], [[Stochastic_Processes_2021_condensed|2021 condensed]], [[Stochastic_Processes_2021.2_2022|2021.2 (2022)]].


[[Category:Lab Macambira]] [[Category:IPRJ]]
[[Category:Lab Macambira]] [[Category:IPRJ]]

Edição atual tal como às 22h51min de 7 de agosto de 2024

This is the main page of an undergraduate-level course in stochastic processes targeted at engineering students (mainly computer engineering and its interface with mechanical engineering), being taught in 2024 (2024.2 period) at the Polytechnic Institute IPRJ/UERJ.


Recent application of Gaussian stochastic processes for 3D motion capture transfer (CVPR 2017)


  • Application to path planning for autonomos cars (see this)
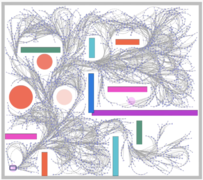  • Application to robot path planning with obstacles (see this)

General Info

  • Instructor: prof. Ricardo Fabbri, Ph.D. Brown University
  • Chat: IRC #labmacambira for random chat

Pre-requisites

  • Undergraduate-level mathematics and probability (will review as needed)
  • Desirable: Intermediate programming experience with any numerics scripting language such as Scilab, Python, R or Matlab. Knowing at least one of them will help you learn any new language needed in the course.

Software

The R programming language and data exploration environment will be used for learning, with others used occasionally. Students can also choose to do their homework in Python, Scilab, Matlab or similar languages. The R language has received growing attention, specially in the past couple of years, but it is simple enough so that the student can adapt the code to his preferred language. Students are expected to learn any of these languages on their own as needed, by doing tutorials and asking questions

  • R studio: recommended IDE for R.
  • Diagrammer: beautiful tool to draw and interact with graphs in R.

Approximate Content

This year's course will focus on a modern approach bridging theory and practice. As engineers and scientists, you should not learn theory here without also considering broader applications. Recent applications in artificial intelligence, machine learning, robotics, autonomous driving, material science and other topics will be considered. These applications are often too hard to tackle at the level of this course, but having contact with them will help motivate the abstract theory. We will try to focus on key concepts and more realistic applications than most courses (that come from the 1900's), that will prompt us to elaborate theory.

Main Resources

Textbooks

Check out the moodle student shelf.

Main book

Introduction to Stochastic Processes with R, Robert Dobrow, 2016 (5 stars on Amazon) Book-R.jpg

Additional books used in the course

Learning stochastic processes will require aditional books, including more traditional ones:

  • Markov Chains: gibbs fields, monte carlo simulation and queues, Pierre Bremaud
  • An Introduction to Stochastic Modeling, Taylor & Karlin
  • Pattern Theory: The Stochastic Analysis of Real-World Signals, David Mumford and Agnes Desolneux - the first chapters already cover many types of stochastic processes in text, signal and image AI Mumford-book.jpg
  • My own machine learning and computational modeling book draft, co-written with prof. Francisco Duarte Moura Neto and focused on diffusion processes on graphs like PageRank. There is a probability chapter which is the basis for this course.

Other books to look at

Basic probability and statistics

  • I recommend you review from the above books. They all include a review. But you might have to see:
  • Elementary Statistics, Mario Triola (passed down to me by a great scientist and statistician)

Interesting books

  • R for data science, O'Reilly (#1 data science bestseller on Amazon) R-oreilly.png

Machine Learning

  • Pattern Theory: From Representation to Inference, Ulf Grenader

Lectures

Lectures roughly follow the sequence of our main book, with some additional material as needed. All necessary background will be covered as needed. Advanced material will be covered partly.

Public Youtube Playlist (Portuguese)

Prof. Fabbri's lectures are publically available online at: 

https://www.youtube.com/playlist?list=PL1tkMA9lsTiVw9PzRcxpUBN4aArh948sK

Partial listing:

Newton PK, Mason J, Bethel K, Bazhenova LA, Nieva J, et al. (2012) A Stochastic Markov Chain Model to Describe Lung Cancer Growth and Metastasis. PLOS ONE 7(4): e34637. https://doi.org/10.1371/journal.pone.0034637

Lecture Notes

  • Fabbri's lecture notes on long term markov chains (based on Dobrow's Chapter 3) pdf

Tentative listing

  • Intro, overview of main processes and quick review
  • Markov Chains
  • Markov Chain Monte Carlo: MCMC
  • Poisson Process
  • Queue theory
  • Brownian Motion
  • Stochastic Calculus

Homework

  • All homework can be done in any language. Most are either in the R programming language or in Scilab/Matlab and Python.
  • If you do the homework in two different languages, you get double the homework grade (bonus of 100%)
  • Late homework will be accepted but penalized at the professor's will according to how late it is
  • All electronic material must be sent to the professors' email, with the string "[iprj-pe]" as part of the subject of the email. You will receive an automatic confirmation.

Assignment 0

  • Exercise 1.1 of the main book
  • Suggested due date: Before thursday of the 2nd week.

Assignment 1

  • Exercise 1 Ch1 of the Pattern Theory book by Mumford & Desolneux,

Simulating Discrete Random Variables (pp 51, 52, 53)

  • No need to read this book for this exercise. You will review discrete random variables in the context of Markov chains for natural language processing; this is basic for most AI bots nowadays. If you're curious about the applications, you can read the book chapter just for fun.
  • Suggested due date: Before Thursday of the 3rd week.

Assignment 2: Exercise list for chapter 1

7 Exercises: 1.3, 1.5, 1.6, 1.7, 1.9, 1.10, 1.19

  • Suggested due date: at least 1 week before P1 (suggested)

Assignment 3: Exercise list for chapter 2

11 Exercises: 2.1, 2.4, 2.6, 2.8, 2.9, 2.10, 2.12, 2.14, 2.15, 2.18 Computer: 2.26

  • Due date: before P1 (suggested)

Assignment 4: Exercise list for chapter 3

Exercises: 3.2, 3.5a-c, 3.10a-d, 3.16i-iv, 3.25a-b, 3.37, 3.58

  • Due date: before P1 (suggested)

Assignment 5: Exercise list for chapter 5 (MCMC)

4 Exercises: 5.1, 5.2, 5.5, 5.6

  • Due date: before P2 (suggested)

Assignment 6: Exercise list for chapter 6

4 Exercises: 6.3, 6.4, 6.7, 6.8

  • Due date: before P2 (suggested)

Exams

  • P1: ter19set23
  • P2: ter17out23
  • Final-Sub: ter19dez2

Evaluation criteria

P = (P1 + P2)/2

if P >= 5 --> passa direto

Trabalhos serão dados após a P1 de acordo com a demanda da turma, sendo a pontuação inclusa na P2.

Final F opcional

M = (F + P)/2 para os que fizerem final

if M >= 5 --> passa
else reprova

Awesome Links

Neural Nets and Stochastic Processes

  • Generative Models for Stochastic Processes Using Convolutional Neural Networks, arxiv, pesquisadores brasileiros (USP)
  • Bayesian SegNet: Model Uncertainty in Deep Convolutional Encoder-Decoder Architectures for Scene Understanding, Cipolla et. al arxiv 2016

Keywords

random fields, stochastic modeling, data science, queue theory, machine learning, poisson process, markov chains, Gaussian processes, Bernoulli processes, soft computing, random process, Brownian motion, robot path planning, artificial intelligence, simulation, sampling, pattern formation, signal processing, text processing, image processing, dimentionality reduction, diffusion, Markov Chain Monte Carlo MCMC, tracking, branching process, stochastic calculus, SDEs

See Also

Previous periods: 2023 (see wiki history) 2022.2, 2021 condensed, 2021.2 (2022).

Disponível em “http://wiki.nosdigitais.teia.org.br/index.php?title=Stochastic_Processes&oldid=41640”