Algebra Linear Numerica 2019

De Pontão Nós Digitais
(Redirecionado de ALN2019)
Ir para navegaçãoIr para pesquisar

Esta é a página oficial do curso de Álgebra Linear Numérica (graduação) do IPRJ, contendo material potencialmente útil ao publico geral.

Informacao Basica

Horario

Atualizado 2019:

  • Tercas 1:20pm-4pm Sala 205
  • Quintas 1:20pm-3:10pm Sala 211
  • Aulas de divudas: Seg 21Out (antes da P1): 4 tempos: 8:50-12:30, e Seg 2Dez (antes da P2): 3 tempos: 8:50-11:30

Avisos

Software

  • Usaremos o Scilab primariamente.
    • Ver funcoes svd, sva, e '\' (barra invertida)
  • Python e Octave sao alternativas aceitaveis

Tarefas e Projetos

As tarefas devem ser formatadas com notacao matematica adequada, preferencialmente em Latex.

Somente serao aceitos arquivos eletronicos no formato PDF ou outro formato aberto como .odt

Quando a tarefa involver qualquer programacao, o aluno devera enviar o codigo fonte. O codigo junto com a documentacao devera estar dentro de um unico diretorio comprimido com .zip ou tar, com o nome do aluno, disciplina e data.

Enviar todo email com a tag "ALNIPRJ" no subject para garantir recebimento.

Tarefa 0 (entrega 29Ago19)

Tarefa 1 (entrega 3Set19)

  • SVD + Scilab
    • Plotar circulo unitario
    • Escolha uma matriz A
    • Transformar cada ponto por A
    • SVD visual: visualizar os eixos e esticamento da transformacao efetuada por A
    • Realizar SVD usando a funcao SVD propriamente dita
    • Repetir com outras matrizes A, aleatorias e nao-aleatorias. Qual o poder de modelagem de matrizes na pratica que voce pode observar assim?
    • Digitar o resultado, preferencialmente em Latex, e entregar por email ou impresso.

Tarefa 2 (entrega 10Set19)

  • Repetir Tarefa 1 para matriz 3x3 em coordenadas homogeneas - modelam rotacoes, translacoes e homografias em 2D de maneira linear em 3D
  • O circulo unitario se transforma para qual objeto?

Tarefa 3: Ajuste de curvas (entrega 17Set19)

Uma das principais aplicações dos métodos numéricos de álgebra linear vistos em aulas consiste na solução de sistemas por mínimos quadrados. Isto, por sua vez, é muito útil para ajustar curvas algébricas (polinomiais) a dados experimentais, por exemplo: encontrar retas, círculos, ou outras cônicas que passam próximos de dado um conjunto de pontos.

  • Ajuste de reta (opcional - para aprendizado apenas)
    • simule a geração de um conjunto sintético de pontos "experimentais" ao longo de uma reta e os perturbe com a função rand() ao longo de cada coordenada
    • use a "barra invertida" '\' do Scilab para gerar a curva que mais se aproxima dos pontos gerados
    • plote seus resultados para diferentes intensidades de ruído
  • Ajuste de cônicas (obrigatorio)
    • simule a geração de um conjunto sintético de pontos "experimentais" ao longo de uma curva polinomial bi-dimensional de grau 2 (círculo, parábola, elipse..) e os perturbe com a função rand() ao longo de cada coordenada
    • use a "barra invertida" '\' do Scilab para gerar a curva que mais se aproxima dos dados gerados
    • plote seus resultados para diferentes intensidades de ruído

Projeto de Reconhecimento de Faces

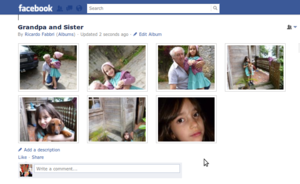
Exemplo de Album com Algumas Faces (Facebook upload)

Album1.png

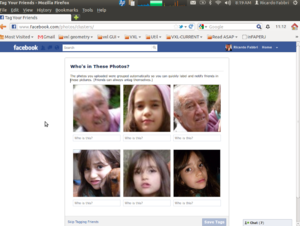
Exemplo de Faces detectadas, a serem reconhecidas no projeto (logo apos Facebook upload)

Album2-faces.png

Procedimento

  • Monte um grupo de colegas, de 2-3 pessoas, para fazer o trabalho: Definir ate 3Set19
  • Baixe este conjunto de bases de dados de faces: RecDev
  • Inicie com a base de dados very-easy. Siga as instrucoes no README
  • Uma vez debugado seu reconhecedor, forneca uma taxa de acerto, usando validacao cruzada separando parte das fotos para treino, parte para teste, e fazendo uma media da taxa de acerto para varias particoes diferentes. Recomendo iniciar com o procedimento retirar 1 foto por pessoa para teste, e usar o restante para reconhecimento, e repetir o processo 10 vezes para comecar. O pseudocodigo fica assim:
 erro_medio := 0
 faca n vezes  // n seria o numero de simulacoes, por exemplo, 10
   bd_treino := base de dados completa (todas as fotos)
   para cada pessoa p
       bd_treino := bd_treino menos uma foto aleatoria da pessoa p
       adicione a bd_teste essa foto aleatoria
   
   treine seu reconhecedor com a base de dados bd_treino
   erro_novo := calcule a taxa de erro testando o reconhecedor nas fotos em bd_teste
   erro_medio := erro_medio + erro_novo
 fim faca
 erro_medio = erro_medio/n
 mostre o erro medio
 bonus: mostre a matriz de confusao
  • Use essa validacao cruzada para melhorar seu reconhecedor. Melhore esse codigo para poder examinar os casos de erro, analise, escreva no seu relatorio sua analise, e tente procurar a fonte do erro e melhorar o reconhecedor.
  • Sera dada maior nota aos alunos que implementarem esse codigo com indices, sem precisar copiar as fotos na memoria para gerar bd_treino e bd_teste. Ao ler imagens, seu codigo tambem devera ser independente do numero de imagens.
  • Uma vez debugado seu reconhecedor e validacao cruzada, rode nas bases easy, medium, hard e extras/facebookfaces e extras/facebookfaces2. Relate seus resultados e dificuldades. Se nao rodar em alguma dessas, ou se o relatorio nao tiver resultados condizentes, a nota sera penalizada.
  • Recomendamos dividir o trabalho da seguinte forma: apos especificar a leitura da base de dados a partir dos arquivos e o formato da base de dados na linguagem, outro colega deve implementar a validacao cruzada.
  • Seu codigo deve funcionar para um numero de fotos diferentes por pessoa. Por exemplo, 5 fotos para a pessoa 1, e 3 fotos para a pessoa 2.
  • Pode assumir que as imagens sao 100x100
  • Codigo para ajudar no trabalho: Rotinas PCA em scilab sip_pca.sci, sip_pca_project.sci. Use a seguinte rotina para aprender a usar este codigo: sip_pca_test.sce
  • Fragmentos de codigo de anos anteriores (so pra ter uma ideia, o seu codigo devera ser muito melhor): aln-src

Entrega do Trabalho

O trabalho devera ser entrege nas seguintes partes:

  • Relatorio
    • Data de entrega: 1 semana antes da P2 até a meia-noite
    • Secoes Obrigatorias:
      • Introducao
      • Descricao clara do problema
      • Descricao da implementacao
      • Mais importante: Descricao do processo de desenvolvimento
        • Experimentos, discussao, analise dos resultados e estudo detalhado dos casos de falha.
      • Conclusao e ideias para trabalho futuro
      • Cada membro do grupo deverá também escrever uma seção de, no mínimo, 2 páginas relatando sua contribuição e experiencia com o trabalho
  • Codigo
    • Data de entrega: 13Mar18 até a meia-noite (melhorias podem ser entregues ate dia 23)
    • Dividir a entrega do codigo em 2 partes:
      • Codigo-fonte
        • README devera incluir instrucoes detalhadas de como rodar o codigo
        • Calcular a taxa de acerto do algoritmo em validacao cruzada
    • melhorias podem ser entregues juntos ao relatorio, desde que, no minimo, o codigo esteja fornecendo uma taxa de acerto e rodando nas bases easy e very-easy

Aviso:

  • Criterio de avaliacao: A nota de trabalho sera dada com base na qualidade do relatorio
  • Bonus #1: O grupo que tiver melhor performance obtera nota 10.0 no trabalho. O segundo melhor grupo obtera um bonus de 2 pontos no trabalho.
    • A taxa de reconhecimento sera medida em uma base elaborada pelo professor durante a correcao, sem o conhecimento previo do aluno. A base de treinamento sera entregue ao aluno no mesmo formato da base recdev acima, no dia 14Mar18
    • A performance para bonus sera medida na presenca do professor, durante processo de correcao em horario de aula no dia 15Mar18, usando-se uma base de teste fornecida no ato. O formato da base de teste sera da seguinte forma:
      • arquivos no formato 
        <id_pessoa>-<id_foto>.jpg
        todas na mesma pasta
      • Por exemplo, 17-3.jpg seria pessoa 17, foto numero 3 da base de teste
      • Este id nao tem relacao com o id usado na base de treino
      • Se houver mais de uma foto teste por pessoa, seu sistema pode usar todas essas fotos para tentar identificar a pessoa
      • Tarefa do seu algoritmo: dadas diversas fotos de uma mesma pessoa desconhecida, do tipo: 
        17-1.jpg, 17-2.jpg, 17-3.jpg, 17-4.jpg, 17-5.jpg
        Qual o id real dessa pessoa 17 na base de treino? Serao apresentadas varias pessoas, e o grupo que acertar mais vence. Nao sera permitido adaptacao do codigo, exceto para mostrar a pasta de teste.
  • O relatorio de cada aluno tambem devera conter um relato da participacao na competicao do bonus, e ira contar na nota do trabalho mesmo se nao ganhar o bonus

Projeto: Análise de Redes Sociais

Neste projeto o aluno coletara uma rede social, por exemplo a rede de amigos do facebook, ou uma rede de troca de mensagens de email, e fara uma análise dos nós mais importantes em relação a PageRank e outras características de difusão na topologia do grafo. Isso poderia ser util, por exemplo, para ordenar a sua lista de amigos por ordem de amigo mais "influente", ou para identificar maneiras de aumentar sua conexao na rede (por exemplo, numa rede de negocios).

Os passos do projeto sao:

  1. Obter sua rede social no formato GML
    1. Redes de troca de emails: http://hera.ethymos.com.br:1080/redes/python/autoRede/escolheRedes.php
    2. Sua rede amigos do facebook: http://snacourse.com/getnet/
  2. Visualizar a rede no software Gephi
    1. Baixe o Gephi em https://gephi.org
    2. Realize o tutorial basico do Gephi (do menu Help)
    3. Abrir o arquivo GML no Gephi
  3. Obter a matriz de Markov dessa rede no Scilab, considerando pesos nas arestas como no algoritmo PageRank
    1. Exportar a rede como matriz de adjacencias no Gephi (aprender como fazer)
  4. Calcular o autovetor dominante (PageRank) no Scilab
  5. Interpretar o que isso pode vir a dizer sobre a importância relativa dos seus amigos na rede de amizades
    1. Por exemplo, a pessoa tem muitos amigos que tem muitos amigos
    2. O que um caminhante aleatório ou quer dizer aqui? Discuta o que um processo de difusao significaria na rede de amizades. Talvez uma rede de indicacoes?
    3. Invente alguma outra medida nessa rede da importancia relativa dos nos


Links interessantes

Conteudo aproximado


Recursos principais

  • Apostila prof. Fabbri
  • Excelente livro recente cobrindo partes deste curso: Applied Linear Algebra, Peter J. Olver and Chehrzad Shakiban
PDF assinado pelos autores para prof. Fabbri
  • Livro classico: "Matrix Computations", Gene Golub et. al. (inventor do algoritimo mais usado de SVD).

Golub-vanloan-thumb.jpg

Outros Recursos

Aulas: Listagem parcial

Para referencia: aulas de Analise Matricial: listagem parcial

Provas

  • P1: 22Out19. Provas anteriores: 2012
  • P2: 3Dez19
  • Final-Sub: 3Dez19-10Dez19 (escolher)

Criterio de Avaliacao

  • Trabalhos: 20% da media - o ultimo trabalho (reconhecimento) valera a metade disto, ou seja, 10% da media
  • O criterio final ficou (favor avisar se precisar adicionar detalhes ou corrigir no caso de erro/discrepancia):

Pessoal, conversei com o professor sobre o erro no critério de avaliação, e, como pedido por ele, estou alterando o valor da média para se passar direto. 

     M_p = (P1 + P2)/2   
     M = 0.8*M_p + 0.2*T (atualizado de 10% para 20% com acordo dos alunos), onde T é a nota dos trabalhos
     Se M >= 5, passou --> M (facilitando: considere T=10,0 no M `a esquerda desta desigualdade aqui)
     prova final - faz quem quiser, mas combinamos que teria de seria feita por quem obtiver M < 5 
          - facilitando: considere T=10,0 e calcule uma media M otimista, para ver se precisa fazer a final. ou seja:

              - Se M_p < 6.25, precisa fazer final! *************************

     M_f = 0.5*(M + P_f) = 0.5*(0.8M_p + 0.2*T + P_f) = 0.2*P1 + 0.2*P2 + 0.5*P_f + 0.1*T
     Se M_f >= 5, passa --> M_f
     Sub: repoe menor de P1, P2, P_f (apenas se alguem faltou alguma prova ou quiser melhorar nota - mas quem entregar ira substituir)
     M_sub = media com sub
     Se M_sub >= 5, passou --> M_sub

     Adendo (em acordo com os alunos): a M_sub = M_f pois sera considerada a mesma prova. Quem for usar a prova como Sub ira substituir a nota independentemente do resultado.

Awesome Links

  • Curso moderno e basico on-line da Brown University sobre algebra linear e aplicacoes [2]
  • Curso on-line da University of Texas at Austin, Linear Algebra - Foundations to Frontiers: Learn the theory of linear algebra hand-in-hand with the practice of software library development [3]

Machine learning com Algebra Linear Numerica

Disponível em “http://wiki.nosdigitais.teia.org.br/index.php?title=Algebra_Linear_Numerica_2019&oldid=41456”